The perfect cube forms ( x y) 3 (xy)^3 (xy)3 and ( x − y) 3 ( xy)^3 (x −y)3 come up a lot in algebra We will go over how to expand them in the examples below, but you should also take some time to store these forms in memory, since you'll see them often ( x y) 3 = x 3 3 x 2 y 3 x y 2 y 3 ( x − y) 3 = x 3 − 3 x 2 y 3
Expand x 2 + y 2-A 2 a b b 2 = 2 x ( x 2 − y 2) 1 / 2 Thus the given expression is identically equal to 2 y ( 2 x x 2 − y 2) x y x − y In the case where x greatly exceeds y, the numerator is essentially 2 y ( 3 x) = 6 x y, and the denominator is approximately 2 xFind the product of two binomials Use the distributive property to multiply any two polynomials In the previous section you learned that the product A (2x y) expands to A (2x) A (y) Now consider the product (3x z) (2x y) Since (3x z) is in parentheses, we can treat it as a single factor and expand (3x z) (2x y) in the same
Expand x 2 + y 2のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
 | 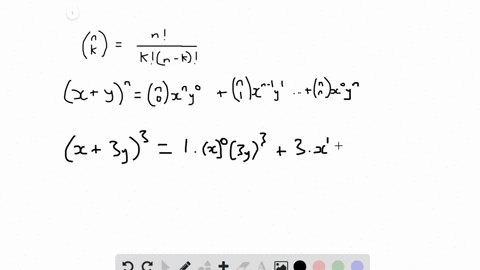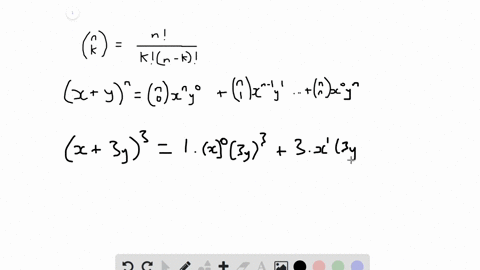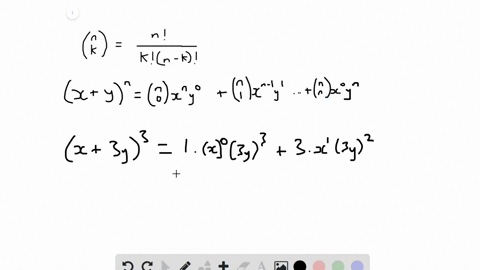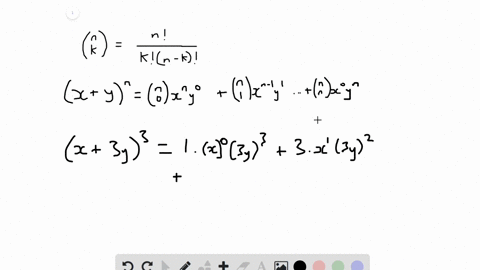 | |
「Expand x 2 + y 2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 | ||
「Expand x 2 + y 2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 |  |  |
「Expand x 2 + y 2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「Expand x 2 + y 2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 | ||
「Expand x 2 + y 2」の画像ギャラリー、詳細は各画像をクリックしてください。
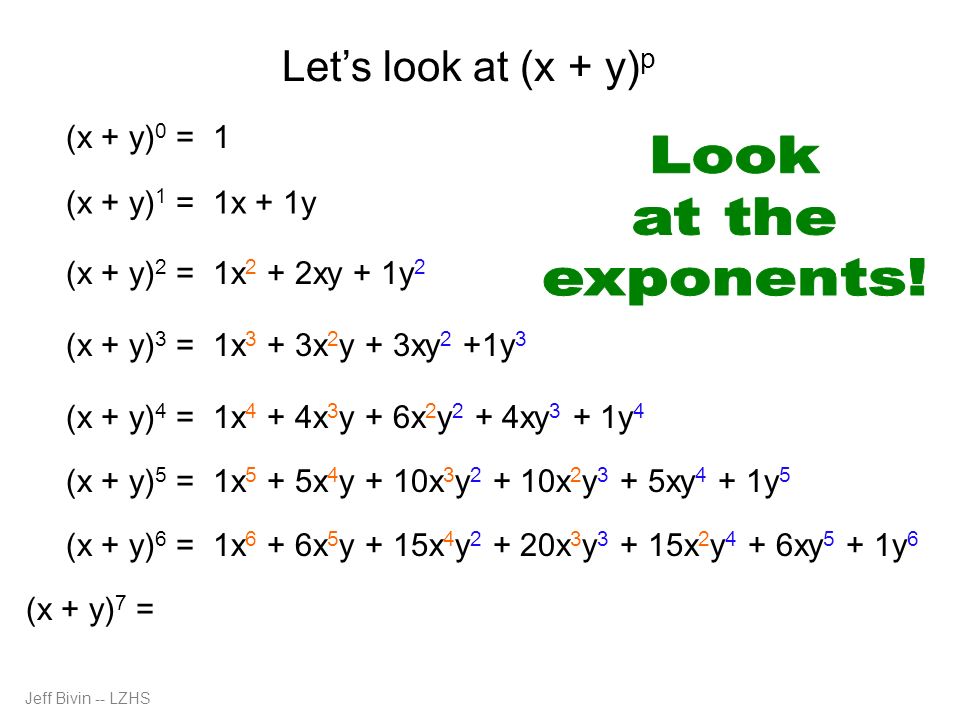 |  |  |
 |  |  |
 |  | |
 |  | 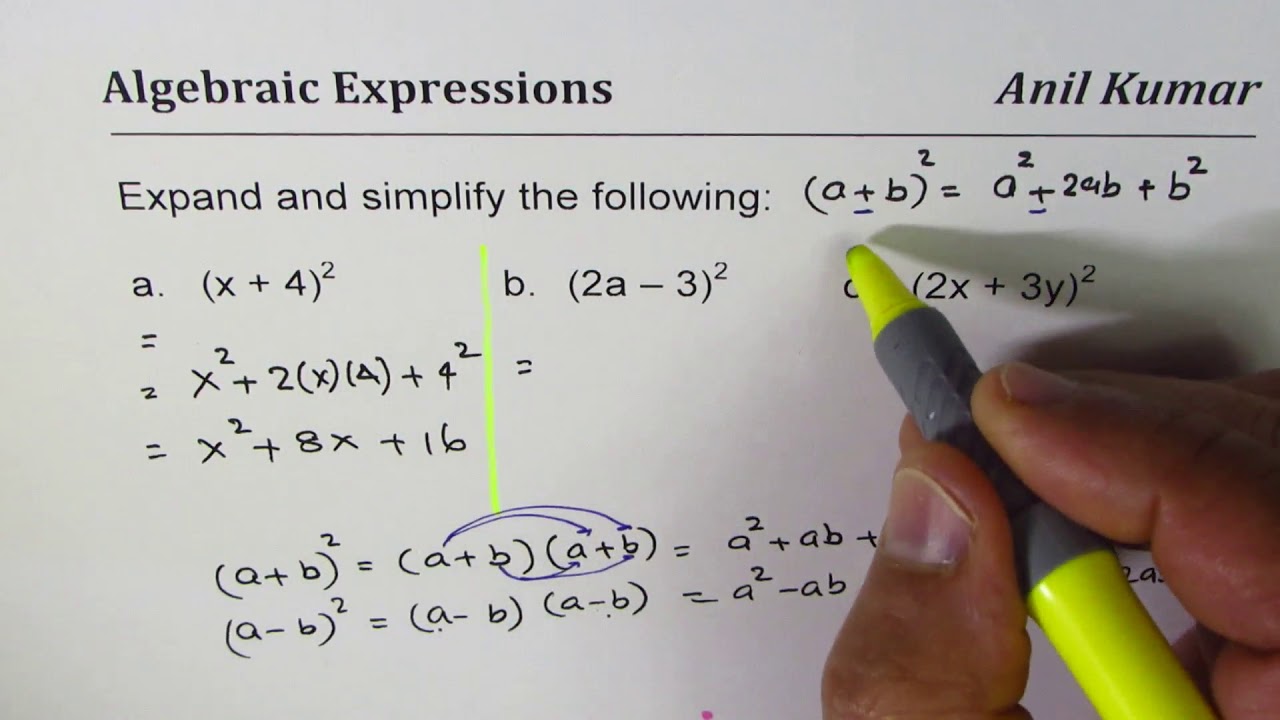 |
「Expand x 2 + y 2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | 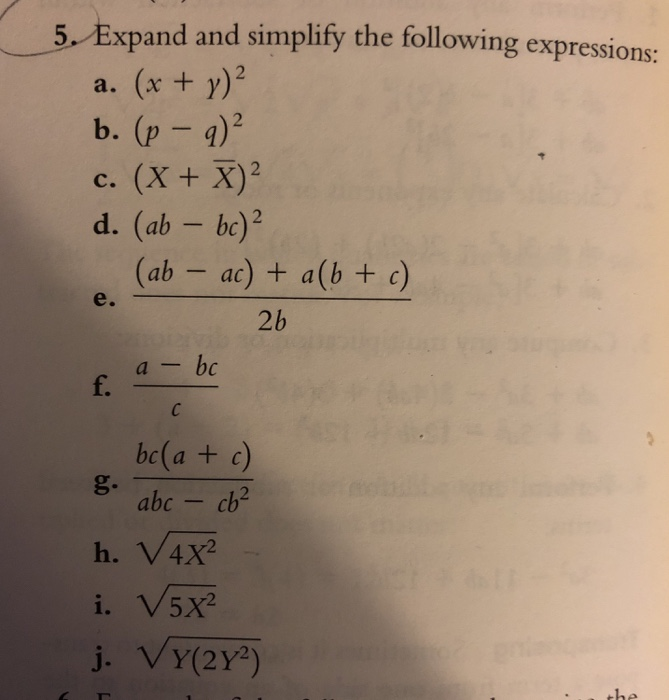 |
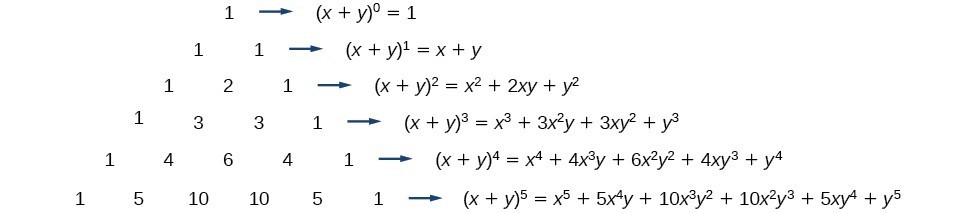 |  |  |
 |  |  |
「Expand x 2 + y 2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | 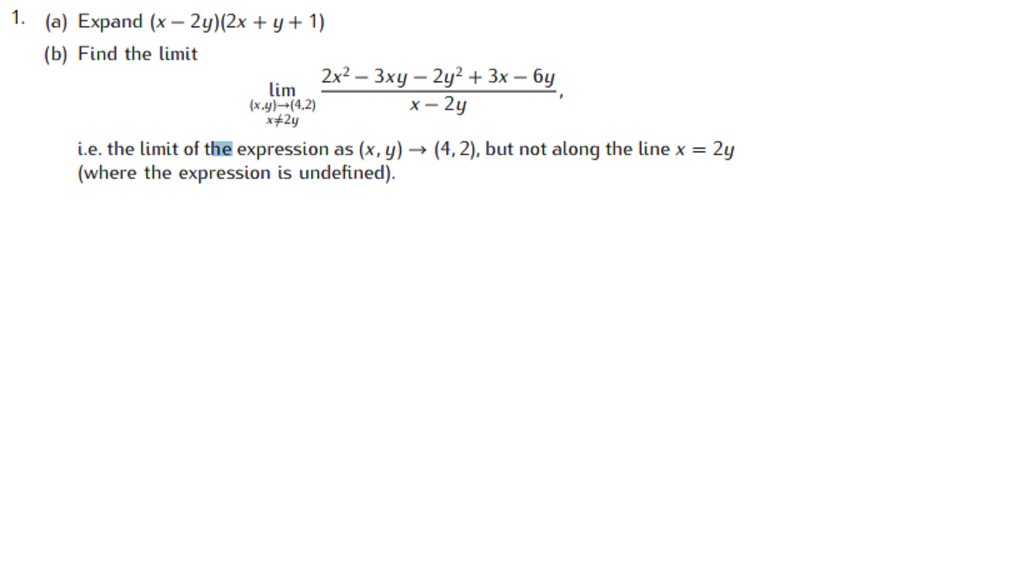 |
「Expand x 2 + y 2」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |
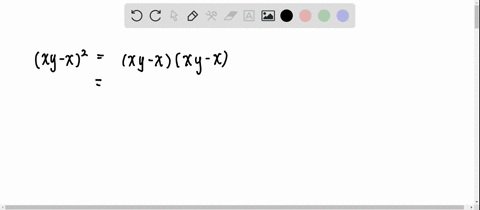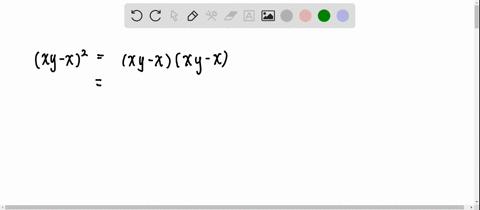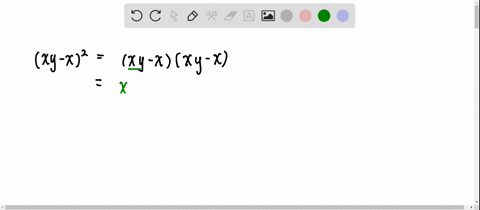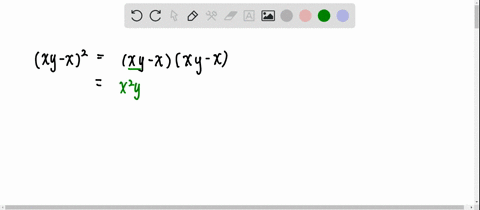
The following are algebraix expansion formulae of selected polynomials Square of summation (x y) 2 = x 2 2xy y 2 Square of difference (x y) 2 = x 2 2xy y 2 Difference of squares x 2 y 2 = (x y) (x y) Cube of summation (x y) 3 = x 3 3x 2 y 3xy 2 y 3 Summation of two cubes x 3 y 3 = (x y) (x 2 xy y 2) CubeRewrite (xy z)2 ( x y z) 2 as (xyz)(xyz) ( x y z) ( x y z) Expand (xyz)(xyz) ( x y z) ( x y z) by multiplying each term in the first expression by each term in the second expression Simplify each term Tap for more steps Multiply x x by x x Multiply y y by y y Multiply z z by z z
Incoming Term: expand x 2 + y 2,



